Trigonometry Formulas

 

Title:  Trigonometry Formulas

Introduction:

Trigonometry, a branch of mathematics that deals with the relationships between the sides and angles of triangles, has been a fundamental part of mathematical knowledge for centuries. Trigonometry Formulas play a crucial role in solving various mathematical problems, particularly those involving angles and distances. In this comprehensive guide, I will try to delve into the essential Trigonometry Formulas, their applications, and how they contribute to solving real-world problems.

Explanation: 

To start today’s article Trigonometry Formulas Let us first know, some key basic concepts of trigonometry.

Listen full article:-

Basic Trigonometric Ratios:

Trigonometry revolves around six primary trigonometric ratios, which are based on the sides of a right-angled triangle. These ratios are sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot). Let's explore each of them:

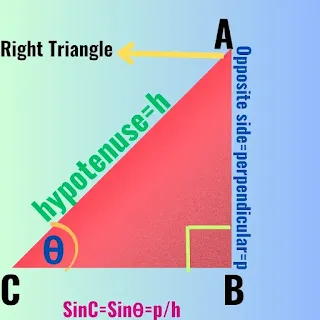
Sine (sinθ):

The sine of an angle in a right-angled triangle is the ratio of the length of the side opposite the angle to the length of the hypotenuse for an angle θ

Sinθ = Opposite side of ∠θ / hypotenuse,which can be expressed as,

Sinθ = p/h, where p = perpendicular and h = hypotenuse of the right triangle.

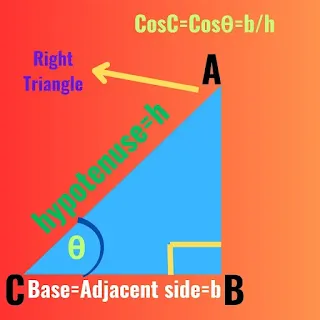
 Cosine (cosθ):

The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse for an angle θ

cosθ = Adjacent side of ∠θ /hypotenuse which can be also expressed,

Cosθ = b/h, where b = base and h = hypotenus of the right triangle.

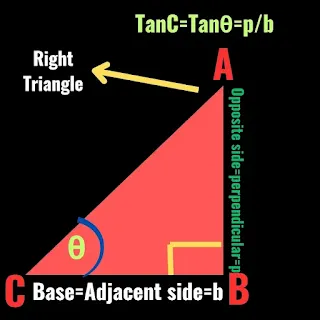
Tangent (tanθ):

The tangent of an angle is the ratio of the length of the side opposite the angle to the length of the adjacent side for an angle θ

tanθ = Opposite side of ∠θ/ Adjacent side which can be also expressed,
tanθ = p/b, where p = Perpendicular and b = base of the right triangle.

 Cosecant (cosecθ):

The cosecant of an angle is the reciprocal of the sine.

cosecθ =1/sinθ

Secant (secθ):

The secant of an angle is the reciprocal of the cosine.

secθ =1/cosθ

Cotangent (cotθ):

The cotangent of an angle is the reciprocal of the tangent.

cotθ =1/tanθ

Pythagorean Identities:

The Pythagorean identities are fundamental trigonometric relationships derived from the Pythagorean theorem. They are expressed as equations involving the sides of a right-angled triangle.

Pythagorean Theorem:

The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (h) is equal to the sum of the squares of the lengths of the other two sides base(b) and perpendicular(p),which is written as,
h² = p² + b²

Pythagorean Identity:

The Pythagorean identity is derived from the Pythagorean theorem and is expressed in terms of trigonometric functions.
sin²α +  cos²α = 1

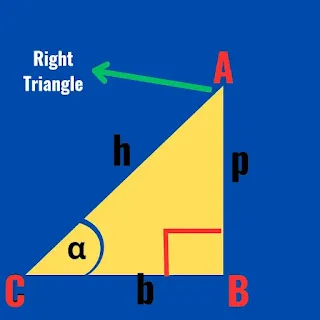
Prove that: sin²α +  cos²α = 1

Answer: 

Let, ABC is a right angled triangle at B
whose, hypotenuse = AC = h
            base = BC = b
          perpendicular = AB = p
and   ∠C = α (Let, us say)
To prove : sin²α +  cos²α = 1
Proof:-
   ∵ ABC is a right angle triangle at B,then according to pythagoras Theorem, we get
 ∴ AB² + BC²  = AC² [ ∵ < B = 90°]
=>AB²/AC² + BC² /AC² = AC² / AC²
 [ ∵ dividing both sides by AC² ]
 =>( p/h)² + ( b/h)² = 1
 => Sin²α + cos²α = 1 Proved.
This identity holds true for all angles and is a foundational relationship in trigonometry.

Reciprocal Identities:

Reciprocal identities are derived by taking the reciprocals of the basic trigonometric ratios.
sinα = 1/cosecα
cosecα = 1/ sinα
cosα = 1/ secα
secα =1/cosα
tanα =1/cotα

Co-function Identities:

Co-function identities are expressed in the relationship between the trigonometric functions of complementary angles (angles that add up to 90 degrees).

 1. Sine and Cosine:

sin(π/2 - θ) = cosθ
cos(π/2 - θ) =sinθ, where θ is an acute angle.

  2.Tangent and Cotangent:

tan(π/2 - θ) = cotθ
cot(π/2 - θ) = tanθ, where θ is an acute angle.

3. Secant and Cosecant:

sec(π/2 - θ) = cosecθ
cosec(π/2 - θ) = sec(π/2 - θ),where θ is an acute angle.

Double-Angle and Half-Angle Formulas:

Double-angle and half-angle formulas are used to express trigonometric functions of angles that are twice or half of a given angle θ or β any one we can assume.

1. Double-Angle Formulas:

sin(2θ) = 2sinθcosθ
cos(2θ) = cos²θ - sin²θ
tan(2θ) = 2 tanθ / (1- tan²θ),where θ is an unknown angle.

2. Half-Angle Formulas:

sin (β/2) = ± √(1-cosβ) /2
cos (β/2) = ± √(1+cosβ) /2
tan(β/2) = ± √(1-cosβ) /(1+cosβ)

Sum and Difference Formulas:

Sum and difference formulas allow the expressions of trigonometric functions of the sum or difference of two angles in terms of the trigonometric functions of the angles themselves.

1. Sum Formulas:

sin(x +y)=sinxcosy + cosxsiny

cos(x +y)=cosxcosy − sinxsiny
tan(x +y)= (tanx + tany) /(1- tanxtany),
where x and y are two different or may be similar angles.

2. Difference Formulas:
sin⁡(x−y)=sin⁡xcos⁡y − cos⁡xsin⁡y
cos(x−y)=cosxcosy + sinxsiny
tan(x−y)= (tanx - tany) /(1+tanx.tany)
where x and y are two different or may be similar angles.

Other Identities of Trigonometry:

1. Sec²θ -Tan²θ = 1
 2. Cosec² - Cot²θ =1

Other formulas of Tanθ and Cotθ:

Tanθ = Sinθ / Cosθ

Cotθ = Cosθ/Sinθ

Some Problems of trigonometry formulas:

Question(1): Prove that, (Cosecθ - Cotθ)² = (1 - Cosθ) / (1+ Cosθ)
Answer: 
          L.H.S =  (Cosecθ - Cotθ)²
                    = (1/ Sinθ - Cosθ/Sinθ)² [ using trigonometry formulas]
                   =  {(1 - Cosθ) /Sinθ}²
                   = (1 - Cosθ)² / Sin²θ
                  = (1 - Cosθ)(1 - Cosθ) / (1- Cos²θ)[using trigonometry formula]
               = (1 - Cosθ)(1 - Cosθ) / {(1)² - (Cosθ)²} 
             = (1 - Cosθ)(1 - Cosθ) /(1 - Cosθ)(1 + Cosθ)
        [ using formula,a² - b² = ( a - b)(a+b)]
            = (1 - Cosθ) /(1 + Cosθ)
           = R.H.S Proved.
Question(2): Prove that, (1 + Sec A) / SecA = Sin²A / 1 - CosA
Answer:  L.H.S = (1 + Sec A) / SecA
                  = (1+1/CosA) ÷(1/ CosA)
                  = {(CosA + 1) / CosA} x CosA
                  = CosA(CosA + 1) / CosA
                 = (CosA + 1) / 1
         = (1+ CosA ) (1- CosA) / 1- CosA  [Multiplying numerator and denominator by (1- CosA)]
= (1 - Cos²A) / 1- CosA [ Applying (a+b)(a-b) =a² - b²]
= Sin²A / 1- CosA [using trigonometry formula]
= R.H.S Proved
Question(3): Show that, 1/(1+Sinθ) +1/(1-Sinθ) = 2Sec²θ
Answer: L.H.S = 1/(1+Sinθ) +1/(1-Sinθ)
                        = (1-Sinθ +1+Sinθ) /(1+Sinθ)(1-Sinθ)
              = 2 /(1- Sin²θ)[Applying (a+b)(a-b) =a² - b²]
             = 2 / Cos²θ [Using trigonometry formula,Cos²θ =1- Sin²θ]
            = 2 x 1/Cos²θ
            = 2 Sec²θ [ Using reciprocal formula]
           = R.H.S Showed.

Applications of Trigonometry Formulas:

Trigonometry has vast spread applications in various fields, and its formulas which are used in solving real-world problems. Some notable applications include:

1. Engineering and Physics:

Trigonometry plays a crucial role in fields such as engineering and physics, where it is used to analyze forces, motions, and waves. The study of oscillatory motion, for instance, heavily relies on trigonometric functions.

2. Navigation:

Navigation, both on land and at sea, relies on trigonometric principles. Navigational instruments use trigonometry to calculate distances, angles, and positions, allowing for precise navigation.

3. Architecture:

Architects always use trigonometry to calculate angles, dimensions, and distances when designing structures. Trigonometric functions play a vital role to ensure the stability and balance of architectural designs.

4. Computer Graphics:

In computer graphics and animation, trigonometry is used to create realistic and visually appealing effects. Understanding trigonometric functions is essential for manipulating shapes and angles in digital environments.

5. Astronomy:

Astronomers use trigonometry to calculate distances between celestial bodies and determine the positions of stars and planets, to  study the geometry of the universe.

Conclusion:

Trigonometry Formulas are fundamental tools in the field of mathematics, providing a systematic way to analyze and solve problems related to triangles and angles. From basic trigonometric ratios to advanced identities, these formulas offer a comprehensive toolkit for mathematicians, scientists, engineers, and professionals in various fields. Understanding and applying these formulas not only enriches mathematical knowledge but also facilitates problem-solving in practical scenarios.....

Click Now

FREQUENTLY ASKED QUESTIONs on Trigonometry Formulas:-

Is trigonometry a triangle?

Answer: Total trigonometry is based on right triangle.The six basic formulas of trigonometry is expressed with the help of right triangle and they can be shown as: Sinθ = Opposite side of an angle θ {perpendicular(p)} / hypotenuse(h) Cosθ = Adjacent side of an angleθ{base(b)} / hypotenuse(h) Tanθ = Opposite side of an angle θ {perpendicular(p)} / Adjacent side of an angleθ{base(b)} Cosecθ = hypotenuse(h) / Opposite side of an angle θ {perpendicular(p)} Secθ = hypotenuse(h) / Adjacent side of an angleθ{base(b)} Cotθ = Adjacent side of an angleθ{base(b)} / Opposite side of an angle θ {perpendicular(p)}

What is sin theta?

Answer: Sinθ is a ratio of opposite side of an angle θ to the hypotenuse of a right triangle, or it is a ratio of perpendicular to the hypotenuse of a right triangle.Mathematically it is written as, Sinθ = Opposite side of an angle θ / hypotenuse = p/ h, where p = perpendicular and h= hypotenuse of right triangle.

What is sin 45 in trigonometry

Answer: In trigonometry Sin45° = 1/√2

What's the value of cos 60?

Answer:The value of cos60° = ½

What are the 3 formulas of trigonometry?

Answer: The 3 formulas of trigonometry are: Sinθ,Cosθ,Tanθ and their reciprocals are: Cosecθ,Secθ,and Cotθ

Share this post: 

Previous

Next